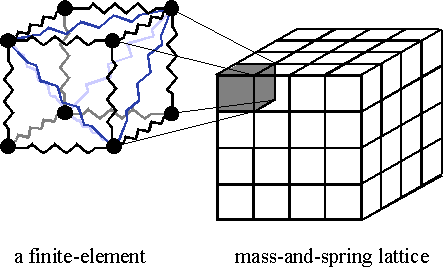
図1 弾性物体の構造モデル
宮崎 慎也 安田 孝美 横井 茂樹 鳥脇純一郎
Modeling and Implementation of Elastic Object Manipulation in Virtual Space
Shin-ya MIYAZAKI, Takami YASUDA, Shigeki YOKOI, and Jun-ichiro TORIWAKI
あらまし 計算機内に構築された仮想環境において,実世界での様々な行動や作業を実現するための技術が注目されている.本文では,非剛体の性質を有する仮想物体に対する自由な操作を実現した例として,仮想空間内でマウスにより制御される棒状のマニピュレータを操作することにより,質点-ばね格子で構成される弾性物体を「打つ」または「突く」といった動作を,実物に近い感覚で実行できる対話操作システムについて述べる.マニピュレータから受ける力学的干渉に対する弾性物体の動的応答は,物理学に基づいたモデルに対する数値的解法により高速に計算され,リアルタイム CG として生成される.弾性物体に過大な外力が加わった場合に対処するために,弾性エネルギーに基づいて振幅に制約の与えられたばねの改良モデルを提案し,実現したシステムによりモデルの有効性を示す.
キーワード 人工現実感,コンピュータグラフィックス,空間操作,弾性物体,ばねモデル
1. まえがき
近年,計算機の演算能力並びにグラフィックスの生成能力が急速に進歩するに伴い,コンピュータグラフィックス(CG)を利用したヒューマンマシンコミュニケーションの新たな可能性が注目されるようになった.複雑な物体の形状や動きを表現するためのCGモデルを高速に計算する高性能プロセッサ,シェーディングやテクスチャマッピング等の高価なレンダリング処理をリアルタイムで実現するグラフィックスエンジンは,高品質のCG映像に対するインタラクティブな操作を実現可能にした.実世界に存在する様々な物体を計算機が人工的に作り出す仮想世界の中に再現し,それらをあたかも実物であるかのように操作できる環境を実現しようとする試みが数多くなされた.しかしながら,それらの研究の多くはハードウェアデバイスの開発に研究の主眼が置かれており[1]〜[9],多様なアプリケーションを実現する上で必要となる仮想環境をソフトウェアにより構築する方法については十分に吟味されてはいない.今後,実用的なアプリケーションを開発していくためには,様々な物理特性をもつ仮想物体に対する対話操作を実現していかなければならない.
本論文では,実世界の物体が有する重要な性質の一つとして弾性を取り上げ,マウスで制御される剛体マニピュレータにより仮想空間内の弾性物体を直接的に操作できる環境を実現した対話操作システムについて述べる.弾性物体の内部や,マニピュレータや床の表面で発生する弾性力を質点とばねの組み合わせにより表現した近似モデルを数値的解法を用いて計算することにより,これらの物体間での力学的干渉による結果の動的応答がリアルタイムCGとして生成される.これにより操作者は仮想空間内において弾性物体を棒で打つ,突くといった操作を実物に近い感覚で実行することが可能となる.
CGアニメーションの分野では弾性物体などの変形物体の動きを生成する手法として,物体の局所的性質に基づく有限個の要素で物体を構成する方法が一般的になっており,有限個の質点とばねを組み合わせた質点-ばね格子は,この方法により弾性物体の内部構造をモデル化したものである.このモデルは限定された範囲の運動が実現できれば良く,かつ十分な計算時間をかけて映像を生成できる場合には有効である.しかしながら,このモデルを入力操作により運動に不確定要素を含み,かつリアルタイム応答を必要とする対話操作の対象として直接用いると,他の物体との強い衝突により弾性物体に過大な外力が加わった場合に,弾性物体を構成している一部のばねの振幅が増大し発散するという問題が生じる.ばねが発散すると格子内の質点の位置が互いに入れ替わるため,格子の構造が局所的に破壊されるという現象が生じる.この問題は,衝突における弾性物体とマニピュレータとの相対速度が大きくなりうる「打つ」,「突く」といった操作では頻繁に生じることになるため,本システムを実現するためにはモデルを改良する必要がある.本文では,弾性物体の一部分に加えられた衝突力のエネルギーを物体内部に分散させることにより,この問題を回避する方法を提案する.
2. 仮想環境のモデル
剛体と比較して弾性物体は,その形状が外力の加わり方により多様に変化するため,打つ,押す,曲げる,捻る,伸ばす,切る等の様々な操作が考えられるが,今回はこれらのうちで最も基本的な,一つの剛体マニピュレータとの跳ね返りにより実現できる「打つ」,「突く」およびそれらの動作が遅い場合である「押す」操作について実現する.また,本研究の目的は物理学に基づいた仮想環境の生成であるので,対話操作の実現に必要となるマニピュレータと弾性物体間の相互作用は力学的干渉に基づいて記述されるべきである.これらの枠組みに基づいてシステムを実現するためには,次にあげる項目を定義する必要がある.
(1) マニピュレータの形状と制御方法
(2) 弾性物体の計算機表現と運動の計算法
(3)弾性物体と剛体面との衝突処理
(4)弾性物体とマニピュレータを含んだ環境
(4)の環境として,ここではリアルタイム操作の実現を考え,剛体平面で構成される十分な大きさの立方体の部屋の中に弾性物体とマニピュレータが1個ずつ存在する最も基本的なものを実現する.
2.2.1 有限要素モデル
弾性物体は計算機処理のために立方体格子の各頂点に質点を,格子の辺及び幾つかの対角線にばねを配置した質点-ばね格子で表現される.文献(15)では,図1下の2種類のばねの配置についてのシミュレーション結果に大きな違いは生じないと述べている.実際,これら2種類に加え,更にこれらを組み合わせた図1上について床やマニピュレータとの跳ね返り運動を視覚的に比較した結果大きな違いは現れなかったので,ここでは単位格子あたりのばねの本数が最も少ない,リアルタイム処理に有利な図1左下の場合を選択した.

図1 弾性物体の構造モデル
2.2.2 弾性物体に働く力の種類
質点-ばね格子で表現される弾性物体が重力場の中で運動する際,格子上の各質点には外力である重力と,弾性物体の内力であるばねの弾性力と減衰力が常に働く.質点 i の質量及び重力加速度ベクトルをそれぞれ mi ,g ,質点 i と質点 j を接続するばねのばね定数,減衰定数,及び自然長をそれぞれ kij ,Dij ,Lij ,質点 i とばねにより接続するすべての質点 j に対する質点 i の相対位置ベクトルを pij ,相対速度ベクトルを vij とすれば,質点 i にかかる力の総和ベクトル Fi は式(1)で表される.
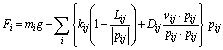 (1)
(1)
更に,弾性物体が他の剛体物体と干渉している間は,弾性物体を構成している質点の剛体内への侵入に対する空間的制約により,2物体間に反発力と摩擦力が発生する.これについては2.3で詳しく述べる.
2.2.3 運動の数値解法
質点とばねが多重に結合した構造体の運動方程式を解くことは困難であり,他の物体と衝突する毎に運動方程式を立て直す必要があるため,弾性物体の動的振る舞いは一般に数値的解法により求められる.質点-ばね格子の各質点において局所的に立てられた運動方程式を時間軸方向に差分近似した式から,時間軸上の離散化された各時刻における質点の速度と位置が得られる.離散時間の間隔をDT とすれば,各時刻 T における質点 i の速度ベクトル Vi (T) 及び位置ベクトル Pi (T) はそれぞれ式(2),式(3)により逐次的に決定される.
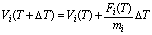 (2)
(2)
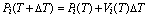 (3)
(3)
この方法は微分方程式の数値解法による近似解の求め方のうちで最も素朴なオイラー法と呼ばれる解法に基づいており,式(2),式(3)はそれぞれ,微小時間DT 間では物体が等加速度運動,等速度運動であるという近似を示しているが,物体の運動の特性を考慮して時間間隔DT を決定できれば十分良い近似解が得られる.運動の形態が基本的に単振動である質点-ばね格子の場合は,DT をばねの振動の周期に対して十分小さくとればよい.
2.3.1 剛体表面の弾性層
弾性物体とマニピュレータ(剛体)間の跳ね返りの強さには,これら両方の物体の性質が反映されるべきである.ここでは剛体側の弾性を表現するために,剛体表面に厚さが一定の薄い弾性をもつ層を仮定する.具体的には,運動計算の各離散時刻において弾性層内に侵入した質点を探索し,それらの質点と層の下面との間にばねを仮想的に配置する(図2).仮想ばねの自然長を層の厚さと等しくとれば,質点の弾性層への侵入量に比例した反発力が質点と剛体表面との間に生じることになる.剛体側の跳ね返りの性質は仮想ばねの弾性係数を変更することにより制御することができる.また,この反発力を2物体間の垂直抗力とすることにより摩擦力も決定できる.
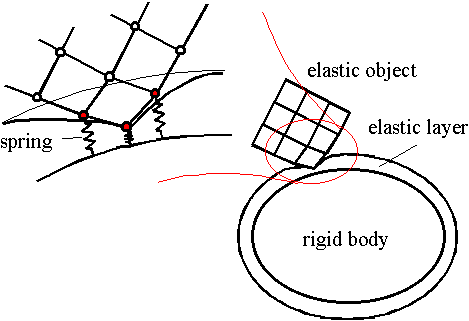
図2 剛体表面に仮定された弾性層
2.3.2 マニピュレータへの反力
マニピュレータを操作し弾性物体に力を加えた際,弾性物体がマニピュレータから受けた力の総和に等しい反力がマニピュレータにも働く.フォースフィードバック機構をもつデバイスを用いた場合,操作者に反力をフィードバックできるが,現システムでは入力デバイスにマウスを用いているので,反力の大きさに応じてマニピュレータの移動量を減らすことにより視覚的に反力のフィードバック効果を与えている.
3. 弾性物体モデルの改善
自然界の物理現象等を計算機を用いて表現しようとする際に数値計算のための近似モデルが適当でないと,精度の良い結果が得られないだけでなく時には実際とはかけ離れた異常な結果となる場合もある.2.で述べた質点-ばね格子モデルによる弾性物体の表現は,実際には連続体であると考えられる弾性物体の運動を短時間の数値計算で実現できるため有効であるが,強い跳ね返り等の比較的大きな外力が作用する場合においては,ばねの線形弾性限界を考慮していないことが原因で格子内でばねの振動が発散してしまい適当でない.本節ではこの問題に対する一つの具体的解決策として,ばねの持つ弾性エネルギーに基づいてばねの振幅に制約を与えることにより,原理的に振動の発散を生じないばねの運動モデルを提案する.
もう一つの振動発散の原因として,物体内部への力の伝搬の遅れがある.弾性物体の表面に加えられた力は実際には瞬時に物体内部へ伝搬するが,数値計算においては離散時間の分解能であるDT の大きさに応じてこの伝搬に遅れが生じる.すなわち,ある質点に加わった外力が i 個先に連結された質点に伝わるのは i DT 後となる.DT の値が大きくなると,この原因による振動発散が生じやすくなる.
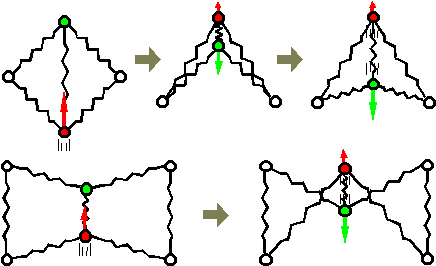
図3 格子内の頂点の入替り
この現象は,下端の質点のみに力が加えられることに起因しているので,下端の質点に加わる力の一部を上端の質点に加える(c)のようなモデルを用いることにより解消できる.モデル(c)では両端点に加わる力を,両端点に等しく加わる剛性の成分と下端のみに加わる弾性の成分に分けることができるので,(c)のモデルは剛体と弾性体の中間的な融合(fusion)モデルと考えることができる.
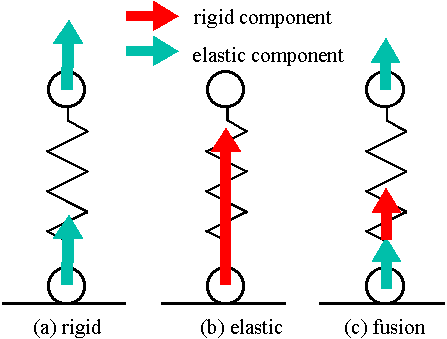
図4 剛性と弾性をもつ3種類のモデル
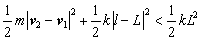 (4)
(4)
左辺の第1項がばねの両端の相対速度 |v2 - v1 | に関する運動エネルギーを,第2項がばねの変位 |l - L | に関する弾性エネルギーを,右辺がばねの変位がばねの自然長と等しくなった時,すなわちばねが伸び(縮み)きった時のばねの弾性エネルギーを示している.式(4)より以下の条件式が得られる.
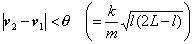 (5)
(5)
これは,ばねの両端の相対速度 |v2 - v1 | がその瞬間のばねの長さ l によって決まるあるしきい値θ以下でなければならないことを示している.
従って,剛性と弾性の比率は,不等式(5)を満たす,すなわちばねの両端の相対速度がθを超えないという条件の下で剛性の比率を最小化するという操作により求めることができる.
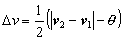 (6)
(6)
これをばねの両端点の速度に互いに逆向きに加えることにより相対速度は許容値まで減少する.
従って,融合モデルの運動計算は通常の弾性モデルの場合の部分的な変更により容易に実現できる.具体的には,式(2),式(3)で示される従来の更新手続き ミ「速度の更新」と[位置の更新」ミ の間に新たに「速度の分散」と呼ぶべき手続きを加えることにより実現される.以下にその手順を示す.
(1) ばねモデルが完全弾性であるとして加速度を計算し,式(2)より各質点の仮の速度を求める.
(2) 両端の相対速度の大きさが不等式(5)を満たさないばねに対して,ばねの両端点の相対速度を減少させるための「速度の修正」を式(6)を用いて行う.
(3) (2)の処理をすべてのばねが不等式(5)を満たすまで反復して行う.
(4) 式(3)の「位置の更新」を通常通り行う.
処理(2)および(3)が付加された手続き「速度の分散」である.これら処理は全体のばねのうちの一部に対してのみ行われるので,これにより生じる処理時間の増加のリアルタイム性への影響は少ない.
融合モデルの有効性を,直列につないだ4本のばねと三角形状につないだ3本のばねの跳ね返りの運動計算の結果により図5,図6に示す.弾性のみのモデル(a) では跳ね返り以降で質点の順序の入れ替わりが見られるが,融合モデル(b) では質点の位置関係が保持されている.

図5 結合された4本のばねの衝突過程
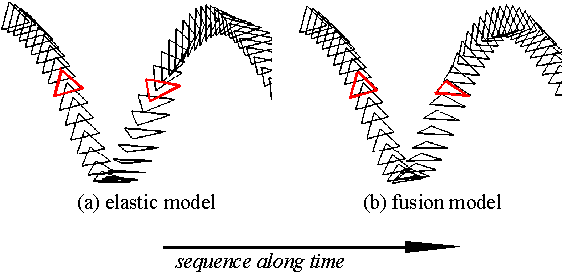
図6 三角形に配置されたばねの衝突過程
4. 実時間処理のためのパラメータ
対話システムを実現する上で,リアルタイム性の検証は重要である.本章ではリアルタイム性が維持可能なパラメータの範囲を実験結果により示す.
n Tc + Tr < Ti , (7)
DT = Ti / n . (8)
また,最近の計算機にはリフレッシュレイトを変更可能なものもあるので,無駄時間が少なくなるようにリフレッシュレイトを選択することも重要である.
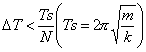 (9)
(9)
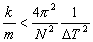 (10)
(10)
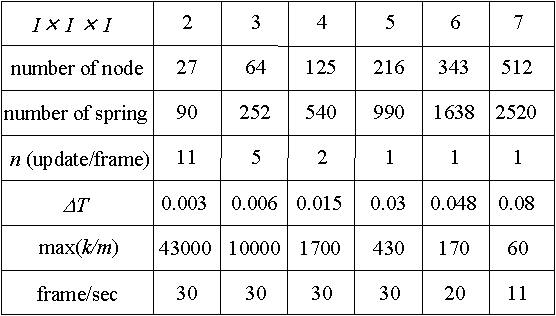
典型的な例として I × I × I の立方体格子によって構成される弾性物体について,標準クラスのグラフィックス機能をもつシリコングラフィックス社製 Indigo2 を使用した場合の,運動計算における実時間処理のためのパラメータの値を表1に示す.毎秒30フレームの映像生成を目標とした場合の n の値から,前述の2つの制約により運動計算がリアルタイムとなるDT の値と,その時に精度良い計算結果が得られるための k / m の上限を決定した.但し,DT のばねの振動の周期 Ts に対する比は10分の1 ( N = 10 ) とした.
格子数 5×5×5 までの場合について毎秒30フレームの映像生成によるリアルタイム性が保証され,少し粗い動きを許容すれば毎秒11フレームの格子数 7×7×7 まで対話性が維持されている.
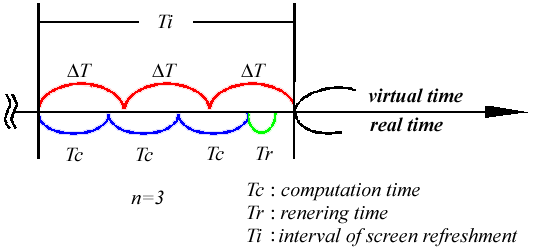
図7 リフレッシュ区間内の実時刻と仮想時刻の配分
5. 実弾性物体とのパラメータ対比に関する考察
仮想弾性物体モデルのもつパラメータ値と実物体のもつ弾性特性値の対比は重要な問題である.質点-ばね格子モデルは弾性物体を表現するための基本的な近似モデルであるため実物体のもつ弾性特性のすべてをパラメータに対比できるわけではないが,ここでは弾性特性のうちで最も基本的なヤング率について,質点-ばね格子モデルのパラメータとの対比を行う.
ヤング率は一方向の変位に対する単位面積当たりの弾性力の量を示すものであり,外力が立方体格子面に垂直に働く場合ならば,力の向きに平行な格子辺上のばねが主に抵抗力を発生するため,質点-ばね格子モデルのばね定数をヤング率に容易に対応させることができる.格子面の対角線上に配置されたばねも抵抗力に貢献するが,簡単のためこれを除外して考えれば,モデルのばね定数 k [dyn/cm] を立方体格子の辺の長さ L [cm] で割ったものが実物体のヤング率 E [dyn/cm2] に相当する.
E = k / L (11)
また,同じヤング率をもつ物体でも比重によって運動は異なる.格子の数が十分多くなれば質量は一様に分布しているとみなすことができるので,各質点の質量を m [g] を L [cm] の3乗で割った値が比重 d [g/cm3] となる.
d = m / L3 (12)
式(11),式(12)により m ,L ,k の比を決定すれば質点-ばね格子モデルのパラメータ値を任意の比重とヤング率をもつ物体に対応させることができるが,4.で示したように k / m の値に上限があるため,実際には L の値に下限が存在する(式(13)).
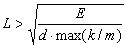 (13)
(13)
式(13)によれば,例えば毎秒30フレーム描画でのリアルタイム処理が可能な最大サイズである 5×5×5 のモデルを用いて比重がおよそ 1 [g/cm3],ヤング率が106[dyn/cm2] であるゴムの弾性を表現するためには,立方体格子の辺の長さを50[cm] 以上にする必要があることになる.これは我々が日常扱う物体の大きさと考えると極めて大きな値である.従って現在の計算機の能力でリアルタイム処理を実現できるのは,ゴムよりもかなりヤング率の小さい柔らかい物体に限定されることになる.しかしながら,計算機能力の問題に関しては,今後の計算機の性能向上や,ばね格子モデルの計算が局所処理に基づいており並列処理が可能であることを考えれば,近い将来ゴムと同程度のヤング率をもつ弾性物体の計算処理をリアルタイムで実現できる可能性は十分にある.
立方体を組み合わせた形状の弾性物体の,対話操作による変形の様子を図8に示す.
 | 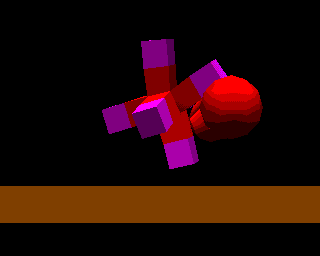 |
 |  |
 | 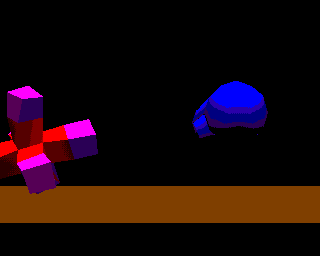 |
図8 弾性物体のマニピュレータや床との跳ね返り
6. むすび
本文では,質点-ばね格子により表現された弾性物体に対するリアルタイム操作を,計算機の処理能力の可能な範囲ではあるが実現した.また,剛体と線形ばねの中間的な性質をもつばねモデルを導入することにより,弾性物体に過大な外力が加わった場合の跳ね返り運動についも実現することができた.本研究は,物理学に基づいてモデル化された仮想世界に対する対話操作を実現した例であり,今後,軟部組織の外科手術や球技スポーツなどの訓練用の対話システムを実現していく上で有効であると考えられる.
今回は物体形状を,ボクセルデータに直接対応する立方体格子の組み合わせに限定したが,今後は自由形状に直接対応できるようなばねの配置の方法も検討していく予定である.
日頃より研究に御援助頂いている中京大学情報科学部の福村晃夫教授に感謝します.なお,本研究の一部は,文部省科学研究費による.