 (1)
(1)
宮崎 慎也 吉田 俊介 安田 孝美 横井 茂樹
Proposal to Model Elastic Objects Based on Maintaining Local Shapes
Shin-ya MIYAZAKI, Shunsuke YOSHIDA, Takami YASUDA, and Shigeki YOKOI
あらまし 弾性応力がばね単位で定義される質点-ばねモデルでは,変形のひずみが大きくなるにつれて弾性応力が物体の平衡形状への復元に有効に作用しなくなる.本文では,質点-ばねモデルの前提である物理学に基づいた局所的性質のモデル化手法を基礎としながら,弾性応力をばね単位ではなく物体を構成する体積的な最小単位である多面体要素単位で定義することにより,変形の度合いが大きな場合にも適当な応力が働き,適正な弾性振動が得られる弾性物体モデルを提案する.物体全体を質点位置に応じて複数の多面体要素に分割し,多面体要素ごとに平衡形状位置,すなわち多面体要素の頂点に配置された質点の弾性振動の収束位置を求め,その位置からの変位に基づいて質点に働く応力を決定する.多面体要素の平衡形状位置は2次元の場合については解析的に,3次元の場合については近似解法を用いて数値的に求める.
キーワード 弾性物体モデル,変形,物理モデリング,対話操作,人工現実感,コンピュータグラフィックス
1. まえがき
仮想空間にCGモデルとして記述された物体を実物のように自由に操作するための技術が注目されている.それらのうち仮想物体の形状を表現するための技術については既に様々なモデル化の方法が提案されており,高性能のグラフィックスハードウェアを用いれば,かなり複雑な形状の物体モデルでさえも実時間応答による対話操作が実現可能である.しかしながら,それらのモデルでは基本的に仮想物体を剛体として扱うことしかできず,弾性変形等の性質を含めてモデル化する方法については満足のいくものは未だ実現されていない.実物体では弾性をはじめとする物理学的性質により外力に対して形状に何らかの変化が生じるのが普通であり,その基本となる弾性物体モデルを実現することは,実用的な仮想空間操作のアプリケーションを実現する上で必要不可欠である.
弾性物体モデルの候補としては,弾性物体を質点とばねの組み合わせにより表現し,物体運動の生成には各質点において局所的に成立する運動方程式を時間軸方向に線形差分することによって得られる漸化式を用いる方法が確立されている[1],[2].この方法は物体運動のシーケンスを比較的高速な計算処理で微小時間間隔で生成できるため実時間処理を要求する対話操作に適した手段であるといえるが,本来,質点-ばねモデルは変位が比較的小さい場合の近似モデルとして,質点間を単純な線形弾性のばねで結んだものであるため,大きな外力が加わるなどして弾性変形のひずみが大きくなると,ばねの弾性振動の発散等により物体の形状が正常に復元しないといった問題を生じる[3],[4],[5].その発生原因は,ばねの振動方向に対して外力が垂直に働く場合と,水平に働く場合の各場合についておおよそ以下のようである.
前者では,個々のばねにおいて,ばねの変位に対して発生する応力の関係が常に線形に定義されていることが原因となる.結果的に振幅が無限に大きな値をとりうることになるため,振幅がばねの自然長を超えると,物体内で質点の位置関係が互いに入れ替わるという異常な状態を招く.後者では,物体の変形に対する復元力をトラス構造に配置された複数のばねが発生する応力の合力により得ていることが原因となる.変形の度合いが大きくなると,すべてのばねが平行に近い位置関係になり,適正な復元力が作用せず,物体の形状復元が正常に行われなくなる.極端な例をあげれば,物体が完全につぶれてすべての質点が同一平面上にある状態では,この平面と垂直な方向への応力は0となり,全く復元しないことになる.
前回の報告では,このうち前者について,振幅が自然長以下に抑制され,弾性振動が発散しないばねの改良モデルを提案した[4].これに対し,ばね自体の改良による後者の原因への対処としては,要素の基本形状に応じた辺および対角線へのばねの配置の仕方の工夫,ばねのパラメータの調節等が考えられるが,複数のばねに関係する問題であるが故に,いずれも根本的な解決策とはなり得ない.
質点-ばねモデルの長所は,実物体の変形の性質がその構成単位である個々の分子のふるまいによるものであることを模倣して,弾性物体の最小構成単位であるばねを局所的性質としてモデル化するのみで物体全体の運動を生成できる点である.反面,物体形状の空間的な復元を要するにもかかわらず,距離という1次元の量を保持するばねを応力発生の最小単位としている点が問題なのである.そこで本研究では,弾性応力をばね単位ではなく物体を構成する体積的な最小単位である多面体要素単位で定義することにより,変形の度合いが大きな場合にも物体形状の復元に適した応力が働き,適正な弾性振動が得られる弾性物体モデルを提案する.
物体全体を質点位置に応じて複数の多面体要素に分割し,多面体要素ごとに平衡形状位置,すなわち多面体要素の頂点に配置された質点の弾性振動の収束位置を求め,その位置からの変位に基づいて質点に働く応力を決定する.例えば,立方体格子の質点-ばねモデルは8つの頂点に質点が配置された立方体が体積的な最小単位となる.多面体要素の平衡形状位置は2次元の場合については解析的に,3次元の場合については近似解法を用いて数値的に求める.
文献[3]では,体積保存という幾何学的制約に基づく臨時の内力を発生させることにより対処している.しかしながら,物体形状の復元を目的とする上では体積が保存されることは形状復元の必要条件でしかない.また,弾性変形において体積が保存されることは一般的ではなく,この点で弾性物体モデルの一般的なモデルとしては問題が残る.
文献[5]では,有限要素法における初期形状という体積的な平衡形状に対して応力を定義する方法を提案しており,この点は評価できるが,有限要素法は本来構造解析を目的とするものであり変位が小さい場合を対象としているため,このモデルでは変位が大きな場合には適正な応力が得られない.
2. 質点-ばねモデル
本文で提案する弾性物体モデルは,質点-ばねモデルにおける弾性応力の定義方法を変更することにより実現している.したがって,本章では提案モデルの基礎となる質点-ばねモデルの弾性運動の計算方法を述べ,3.で提案モデルにおける弾性応力の定義方法について述べる.
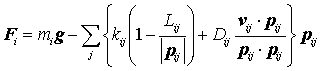 (1)
(1)
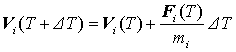 (2)
(2)
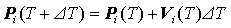 (3)
(3)
ここで, DT の値は,ばねの振動周期に対して十分小さくとる必要がある.
これは,跳ね返りによる質点の速度変化が,更新時刻間隔 DT に対して十分短い時間に行われるという仮定に基づいている.したがって,たとえ被衝突面が理想的な剛体面でなくとも,弾性物体の弾性係数に対して被衝突面の弾性係数が十分大きい場合ならば,衝突における質点速度の反転に要する時間は弾性物体の振動周期に対して十分短いので,反発係数を変更することにより上記のモデルで異なる硬さの剛体面との跳ね返りを表現できる.
ただし,上記の跳ね返り処理は弾性物体を構成する各質点と剛体面との干渉判定が行われた後の処理である.実用化においては干渉判定処理の高速化や弾性物体同士の衝突処理等も必要となるであろうが,これらの内容については本論文の範囲外とする.
3. 弾性多面体要素モデル
そこで,図1(a)および図2(a)に示すように,格子の体積的な基本要素となる多面体要素ごとに,多面体の平衡形状の位置を求め,それに対する各頂点の変位に比例した力をその頂点に働く応力とするようなモデル(以下多面体要素モデル)を考える.多面体要素モデルは,実物体の弾性応力が分子間力に基づいているという事実を模倣して,局所的性質を定義することにより全体の弾性運動を生成するというばねモデルの基本方針を継承し,かつ本来の目的である平衡形状への復元を基準とした応力の定義方法を与えることにより,従来の長さという1次元量に基づいた応力定義による問題点を克服している.これが多面体要素モデルの基本原理である.
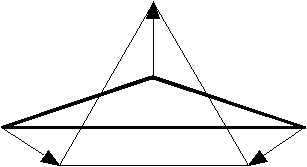
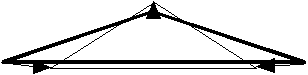
(b) a combination of three springs
図1 極度に変形した正三角形要素に働く応力
Fig.1 A set of stress for an extremely deformed regular triangle.
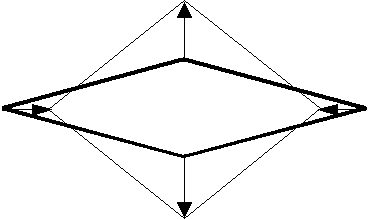
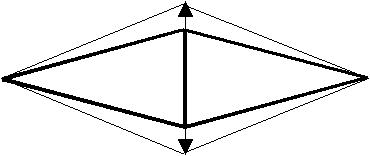
(b) arranging a spring on a vertical diagonal
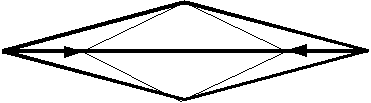
(c) arranging a spring on a horizontal diagonal
図2 極度に変形した正方形要素に働く応力
Fig.2 A set of stress for an extremely deformed regular squre.
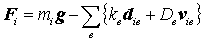 (4)
(4)
次節以降では,形状復元に適した多面体要素の応力を決定するために必要となる,多面体要素ごとの平衡形状位置を求める方法について述べる.
したがって,ある瞬間の多面体の頂点 i の,平衡形状での重心に対する相対ベクトルを Ri ,変形形状でのそれを ri とすれば,式(4)における頂点 i の変位ベクトル die は ( ri -Ri )で与えられるので,{ ri }を既知,{ Ri }を未知とする力のモーメントの釣り合いの方程式
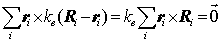 (5)
(5)
を解くことにより,多面体の平衡形状位置および頂点に働く応力が一意に定まる.
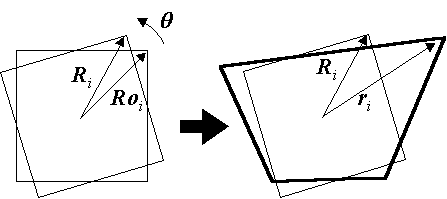
実際の計算処理では,Ri の初期状態 Roi を記録しておき, Ri は Roi を重心周りに回転させたものであることから(図3),Roi から Ri への回転を与える変換行列を M として,{ ri }および{ Roi }を既知, M を未知とする以下の方程式を解くことになる.
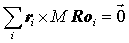 (6)
(6)
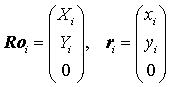 (7)
(7)
という形で与えられる.また,回転行列 M は xy 平面上での原点周りの回転となるので,その回転角度を未知変数q として
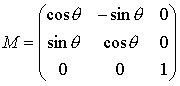 (8)
(8)
とおける.式(7),式(8)の変数を式(6)に代入,整理して得られる以下の式から cosq , sinq の値が定まり,回転行列 M ,{ Ri }が順に定まる.
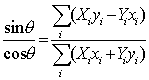 (9)
(9)
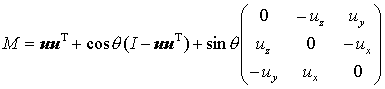 (10)
(10)
となる[6].ただし, ux2 + uy2 + uz2 = 1 である.
ここで,式(6)を解析的に解いて軸ベクトル u および回転角度 q の解を得ることは困難であるため近似解法を用いる必要がある.ここで,時刻 T の{ Ri }を求めるために,式(6)の{ ri }および{ Roi }として時刻 T の{ ri }および時刻 ( T - DT ) の{ Ri }を用いることを考える.すなわち
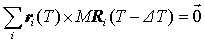 (11)
(11)
を解く上では q ≒ 0 が適用できるので,既知変数
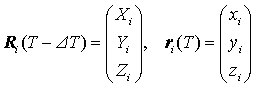 (12)
(12)
と,近似式 cosq = 1,sinq = q を式(10)に代入した結果の M を式(11)に代入することにより以下の式を得る(詳細は付録2.参照).
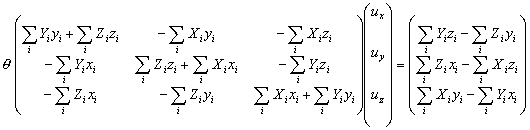 (13)
(13)
式(13)から得られる ux : uy : uz から正規化された軸ベクトル u が定まり,次に回転角度 q が定まる.
図4は三角形要素を組み合わせてできる2次元形状および3×3×3の立方体格子の3次元形状について,要素形状に基づいた応力(上段)とばねによる応力(下段)の各場合について運動計算の結果を,弾性物体の硬さを示す質点の質量mに対する弾性定数kの比k/mを同一にした場合で比較したものである.(a)では,ばねモデルの場合に応力が適当でないために一部質点位置の入れ替わりが生じている.(b)は,弾性係数が比較的小さい柔らかい物体が床に衝突した直後の状態であるが,ばねモデルでは床に近い一列が内部に入り込んだ状態になっている.(c)は(b)と比較してk/mの値が大きい場合で床との衝突のみではばねモデルでも形状の破綻は生じなかったが,対話操作により外力を加えた結果,ばねモデルでは質点の入れ替わりが繰り返され,すべての頂点が中央に集まった状態になっている.
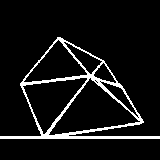 |  |  |
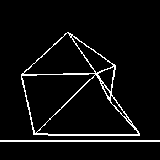 |  |  |
| (a)k/m=104 | (b)k/m=104 | (c)k/m=105 |
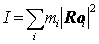 (14)
(14)
を用いれば,各離散時刻における瞬間の近似誤差による角加速度aは
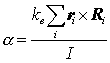 (15)
(15)
となる.
表1は,単一の立方体要素が一辺の長さの 10 倍程度の高さから落下し,剛体の床と初めて衝突した直後から 10 秒間の各離散時刻における式(15)の角加速度 a の平均値 m(a),標準偏差 s(a) および最大値 max(a) を,弾性物体の硬さを示す k / m を現実的な値[4]である 104,105,および106 とした各場合について示したものである.このうちA列およびB列は, DT の大きさを弾性振動の周期の 10分の1 および 100分の1 程度とした場合であり,これらの結果から DT が大きくなると近似誤差が無視できなくなることがわかる.逆に DT を小さくすれば式(10)の q の値が小さくなるので近似誤差は減少するが, DT の値に反比例して計算時間が増加するという問題が生じる.そこで DT の値を変化させずに近似誤差を減少させる方法を以下に提案する.
式(11)ではq ≒ 0 という条件を満たすために,式(6)における参照形状{ Roi }として{ Ri (T - DT ) }を採用した.これにより得られる{ Ri }は近似解法であるため真の値とはならないが,少なくとも{ Roi }よりは真値に近いことが期待できる.すなわち,式(11)より得られた{ Ri (T ) }を{ Roi }として再度式(6)を解くことにより,更に真値に近い{ Ri }が得られることがわかる.このように考えると,式(6)を1回解く操作は{ Ri }を真値に近づける操作であると解釈できるので,{ Ri (T- DT ) }を初期値として上記の手順で式(6)を反復して解くことにより,{ Ri }の値は真値に収束していくと考えられる.
表1のC列,D列の部分は, DT の値をA列と等しくし,上記の反復回数を2回および3回とした場合の近似誤差である.反復を繰り返すごとに近似誤差が著しく減少している.また,これらの結果は立方体要素1個の場合であり,複数の要素が結合した状態では個々の要素の重心回りの回転は近傍の要素により抑制されるため,近似誤差の実際の影響はさらに小さいと考えられる.したがって実用上は反復回数2回で十分である.
反復回数を固定すれば,ばねモデルと多面体要素モデルの計算量はいずれも弾性要素数に比例するので,両モデル間で計算時間の本質的な差はないといえる.シミュレーション実験の結果でも,ばねモデルの計算時間を基準として,多面体要素モデルの計算時間は反復回数2回の場合で5%程度の増加であることが確認されている.
k/m = 104
| A | B | C | D | |
|---|---|---|---|---|
| number of iteration | 1 | 1 | 2 | 3 |
| DT | 0.006 | 0.0006 | 0.006 | 0.006 |
| m(a) | 4.52554 | 0.032915 | 0.000493 | - |
| s(a) | 4.49862 | 0.037503 | 0.002110 | - |
| max(a) | 30.875971 | 0.320008 | 0.060352 | 0.000001 |
k/m = 105
| A | B | C | D | |
|---|---|---|---|---|
| number of iteration | 1 | 1 | 2 | 3 |
| DT | 0.002 | 0.0002 | 0.002 | 0.002 |
| m(a) | 1.987712 | 0.030974 | - | - |
| s(a) | 1.683120 | 0.028445 | 0.000001 | - |
| max(a) | 9.119262 | 0.157926 | 0.000017 | - |
k/m = 106
| A | B | C | D | |
|---|---|---|---|---|
| number of iteration | 1 | 1 | 2 | 3 |
| DT | 0.0006 | 0.00006 | 0.0006 | 0.0006 |
| m(a) | 1.301888 | 0.005511 | - | - |
| s(a) | 1.297613 | 0.005129 | - | - |
| max(a) | 7.570902 | 0.034552 | - | - |
5. むすび
本論文では,従来の質点-ばねモデルにおけるばねに基づく弾性応力の定義を拡張し,弾性物体を構成する多面体要素の形状に基づいて弾性応力を定義した弾性物体モデルを提案した.
今回の報告では,自由形状を多面体要素に分解する方法については触れなかったが,弾性運動の計算処理時間が高コストであることを考えると,少ない多面体要素数で効果的な弾性物体運動を実現することが今後の課題となる.物体形状の与え方として,立方体格子に対応するボクセル表現を採用すれば実現は容易であるが,複雑な形状を表現するためにはボクセル分割の解像度をあげる必要があるため実時間処理を考えると限界がある.物体の形状に適した効果的な要素分割には多面体要素の形状を任意にとれる方が有利であるので,その際には多面体要素の形状にかかわらず常に適正な応力が得られる本モデルは有効な手段となる.また,本モデルは変形の度合いが比較的大きくなる柔軟な弾性物体が表現できるため,軟部組織の外科手術や球技スポーツなどの訓練用の対話システムへの応用も有効である.
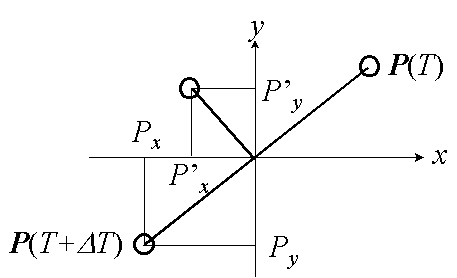
理想的な質点と剛体面との跳ね返りでは,質点は剛体面と垂直なある2次元平面上を運動することになる.この平面上において以下のに示すような,衝突点を原点,剛体面と平行な方向を x 軸,垂直な方向を y 軸とする座標系を考え,この座標系における修正前の速度ベクトル V(T+DT ) および位置ベクトル P(T+DT ) の2次元の座標値を (Vx , Vy ) および (Px , Py ) とする(図A-1).また,これらの衝突処理による修正後の座標値を (Vx' , Vy' ) および (Px' , Py' ) で表す.衝突の前後において質点速度の y 成分は質点と剛体面との反発係数 e に応じて減速かつ反転する.
Vy' = - e Vy
Py' = - e Py
また,質点と剛体面との摩擦係数をmとし,衝突時に質点 i と剛体面との間に発生する垂直抗力を mi (1+e)Vy とみなせば,質点速度の x 成分は以下の式により減少または 0 となり,質点速度は減速または停止する.
Vx' = Vx-m(1+e)Vy
Px' = Vx'DT
ただし Vx と Vx' の積が負となる場合は Vx' および Px' は共に零ベクトルとなる.
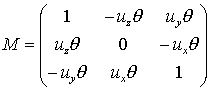
で与えられ,これと式(12)の既知変数を用いれば,
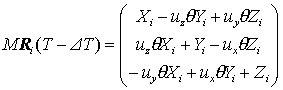
となる.これと式(12)の既知変数を用いて式(11)を表すと,
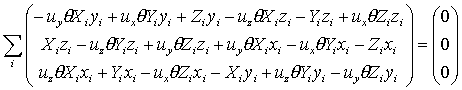
となる,この等式の左辺の項のうち q を因数にもたないものを右辺に移項し, q , ux , uy ,および uz について整理すると式(13)が得られる.