 |  |
| (a) 愜傝曉偟 | (b) 愜傝嬋偘 |
 | |
| (c) 愜傝崬傒 | |
恾侾丂俁庬椶偺婎杮愜傝
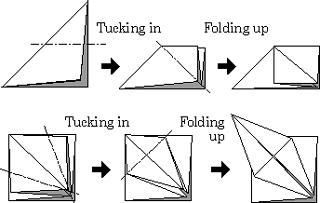
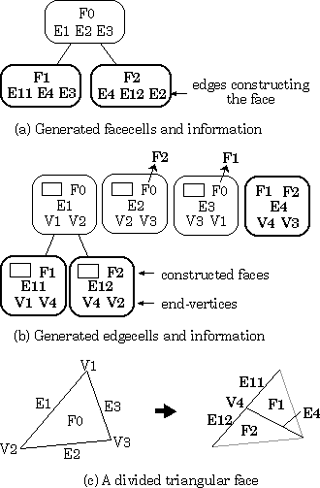
恾俀丂婎杮愜傝偺慻傒崌傢偣偵傛傞暋嶨側愜傝曽
媨嶈 怲栫丂埨揷 岶旤丂墶堜 栁庽丂捁榚 弮堦榊
僌儔僼傿僢僋僗僴乕僪僂僃傾偺恑曕偵敽偄丆僌儔僼傿僢僋僗娐嫬傪梡偄偨恖娫偵恊偟傒傗偡偄僸儏乕儅儞僀儞僞僼僃僀僗偺峔抸偑壜擻偵側偭偰偒偰偄傞丏CG偵傛傞價僕儏傾儖側娐嫬傪棙梡偡傟偽丆僐儞僺儏乕僞撪偵掕媊偝傟偨壖憐嬻娫拞偺暔懱傪幚暔偲摨偠傛偆偵憖嶌偡傞偙偲偑壜擻偵側傞丏杮榑暥偱偼丆壖憐嬻娫拞偵昞尰偝傟偨巻偵懳偟乽愜傝嬋偘乿乽愜傝曉偟乿乽愜傝崬傒乿偺懳榖憖嶌偑壜擻側愜傝巻偺僔儈儏儗乕僔儑儞僔僗僥儉傪奐敪偟偨偺偱曬崘偡傞丏僆儁儗乕僞偼僗僋儕乕儞儌僯僞乕偵昞帵偝傟偨俁師尦壖憐嬻娫撪偺巻傪儅僂僗僨僶僀僗偵傛傝巻柺偺捀揰傪揈傑傫偱堏摦偡傞姶妎偱憖嶌偱偒傞偺偱丆幚暔傪愜傞傛偆側姶妎偱壖憐偺巻傪帺桼偵愜傞偙偲偑偱偒傞丏偙偺憖嶌偼帇揰堏摦偵傛傝巻傪偁傜備傞曽岦偐傜娤應偟側偑傜峴側偆偙偲偑偱偒丆偙偺憖嶌傪孞傝曉偡偙偲偵傛傝堦枃偺巻傪暋嶨側宍忬偵梕堈偵壛岺偱偒傞丏傑偨丆捀揰傗曈摨巑傪惓妋偵廳偹偰愜傞応崌偵偼偦傟傜偺旝柇側偢傟偼帺摦揑偵曗惓偝傟傞偺偱丆幚嵺偵巻傪愜傞傛傝傕惓妋偐偮梕堈偵壖憐嬻娫偺巻傪愜傞偙偲偑偱偒傞丏杮暥偱偼僔僗僥儉偺幚尰偵偍偄偰摿偵廳梫側丆巻柺偺愙懕傗廳側傝娭學摍偺愜傝巻偺忬懺傪俀暘栘儕僗僩偵傛傝婰弎偡傞曽朄丆愜傝憖嶌偵廬偭偰儕僗僩傪崅懍偵曄峏偡傞曽朄丆儅僂僗擖椡偵傛傝俁師尦嬻娫撪偵偁傞巻偺捀揰偺埵抲傪堏摦偡傞偨傔偺岺晇側偳偵偮偄偰傕弎傋傞丏
Shin-ya Miyazaki, Takami Yasuda, Shigeki Yokoi, and Jun-ichiro Toriwaki With advance of graphics hardwares, possibility of natural man-machine interface using graphic environments is drawing attention. Visual environments using computer graphics are very effective for virtual object manipulation. This paper describes a visual simulation system of ORIGAMI (paper folding art) which realizes interactive folding operations of paper such as 'Bending,' 'Folding up' and 'Tucking in' in real-time. In the system, a piece of virtual paper is defined in a three dimensional (3D) virtual space and displayed on a graphic screen. An operator can fold it freely and iteratively into complex figure, observing it from an arbitrary direction and manipulating it as if he is folding a real paper, by picking and moving a vertex of the paper using a mouse device. If the position of the picked vertex is different from operator's intentional position delicately, it is corrected automatically in the case of matching the picked vertex to another vertex or matching two edges to each other. This function has the operator fold a virtual paper more rapidly and accurately than folding a real paper. This paper also presents how to represent the state of folded paper such as connectivity and overlap relation between paper faces and how to realize interaction using a mouse device in the system.INTERACTIVE MANIPULATION OF ORIGAMI IN 3D VIRTUAL SPACE
1. 傑偊偑偒
僌儔僼傿僢僋僗儚乕僋僗僥乕僔儑儞偺惈擻偑媫懍偵恑曕偟夋憸偺惗惉懍搙偑岦忋偡傞偵敽偄丆僌儔僼傿僢僋僗娐嫬傪棙梡偟偨僸儏乕儅儞儅僔儞僐儈儏僯働乕僔儑儞偺怴偨側壜擻惈偑拲栚偝傟傞傛偆偵側偭偨丏儕傾儖僞僀儉偱崅懍偵惗惉偝傟傞僐儞僺儏乕僞僌儔僼傿僢僋僗傪棙梡偡傟偽丆僆儁儗乕僞偼僐儞僺儏乕僞撪偵掕媊偝傟偨壖憐揑側俁師尦悽奅偺暔懱傪幚暔傪憖嶌偡傞傛偆側姶妎偱憖嶌偡傞偙偲偑壜擻偲側傝丆愝寁丆屸妝丆嫵堢丆孭楙側偳傪偼偠傔偲偟條乆側暘栰傊偺墳梡偑婜懸偝傟偰偄傞丏壖憐悽奅偺暔懱偵懳偟偰幚暔偲摨偠條側憖嶌傪峴側偆尋媶偼悢懡偔曬崘偝傟偰偄傞偑丆偦傟傜偺傎偲傫偳偼暔懱偲偺僀儞僞儔僋僔儑儞偺嵺偵嬻娫撪偺暔懱埵抲傪惓妋偵巜掕偟偨傝丆椡妎傪僼傿乕僪僶僢僋偟偨傝偡傞偨傔偺擖椡僨僶僀僗偺奐敪偵廳揰傪抲偄偰偍傝丆僜僼僩僂僃傾偵傛傞壖憐暔懱偺婰弎傗憖嶌側偳偵娭偟偰偼崉懱偺堏摦傗愗嶍偵傛傞慪惈慺嵽偺壛岺側偳扨弮側傕偺偑傎偲傫偳偱偁傞[1] - [8]丏偙偺傛偆側壖憐嬻娫憖嶌傪條乆側暘栰傊揔梡偟偰偄偔偨傔偵丆崱屻偼傛傝暋嶨側惈幙傪帩偮壖憐暔懱傪僐儞僺儏乕僞撪偵掕媊偟丆壖憐暔懱偲偺條乆側僀儞僞儔僋僔儑儞傪幚尰偟偰偄偔偙偲偑昁梫偲峫偊傜傟傞丏
杮榑暥偱偼丆巻偲偄偆斾妑揑扨弮偱偼偁傞偑愜傟嬋偑傞偲偄偆惈幙傪傕偮旕崉懱偺慺嵽傪懳徾偲偟丆俁師尦偺壖憐嬻娫偵懚嵼偡傞侾枃偺巻傪帺桼偵愜傞僾儘僙僗傪儕傾儖僞僀儉憖嶌偱幚峴偱偒傞僔儈儏儗乕僔儑儞僔僗僥儉傪奐敪偟偨丏僆儁儗乕僞偼儕傾儖僞僀儉偱曄壔偟偰偄偔壖憐嬻娫偺忬懺傪僗僋儕乕儞傪捠偟偰儌僯僞乕偟側偑傜丆儅僂僗僨僶僀僗偱惂屼偝傟傞嬻娫撪偺憖嶌揰傪巊偭偰巻偺捀揰傪揈傑傫偱帺桼偵堏摦偱偒傞偺偱丆幚暔偺巻傪愜傞傛偆側姶妎偱壖憐偺巻傪愜傞偙偲偑偱偒傞丏婎杮揑側愜傝曽偲偟偰乽愜傝嬋偘乿乽愜傝曉偟乿乽愜傝崬傒乿偺俁庬椶傪梡堄偟丆偙傟傪慻傒崌傢偣傞偙偲偵傛傝巻傪暋嶨側宍忬偵梕堈偵壛岺偱偒傞丏帇揰偼儃僞儞憖嶌偵傛傝忢帪曄峏偑壜擻偱偁傝丆愜傝巻傪偁傜備傞曽岦偐傜娤嶡偟側偑傜憖嶌偑峴側偊傞丏峏偵丆捀揰傗曈摨巑傪惓妋偵廳偹偰愜傞応崌偵偼偦傟傜偺旝柇側偢傟偼帺摦揑偵曗惓偝傟傞偺偱丆幚嵺偵巻傪愜傞傛傝傕惓妋偐偮梕堈偵壖憐嬻娫偺巻傪愜傞偙偲偑偱偒傞丏傑偨丆杮僔僗僥儉偼壖憐揑側嬻娫偵懳偡傞帺桼側憖嶌傪幚尰偟偰偄傞偨傔丆僨乕僞僌儘乕僽傗僿僢僪儅僂儞僩僨傿僗僾儗僀 (H.M.D.) 側偳偺僨僶僀僗傪梡偄傞偙偲偵傛傝恖岺尰幚姶僔僗僥儉傊偺墳梡傕壜擻偱偁傞丏
2. 愜傝巻僔儈儏儗乕僞
杮僔僗僥儉偱偼丆巻偺侾偮偺捀揰傪堏摦偡傞偙偲偵傛傝侾夞偺愜傝憖嶌傪巜掕偡傞丏杮復偱偼偙偺婎杮憖嶌偵傛傝幚尰偝傟傞愜傝曽偺庬椶偲偦偺擖椡曽朄丆媦傃偦傟傜傪幚尰偡傞偨傔偵昁梫偲側傞僔僗僥儉偺張棟偵偮偄偰弎傋傞丏
(2) 愜傝崬傒 (Tucking in)
傕偆侾偮偺愜傝曽偲偟偰丆偁傞柺傪嫬偵柺偺夞揮曽岦偑堎側傞乽愜傝崬傒乿偑梡堄偝傟偰偄傞丏乽愜傝崬傒乿偼乽愜傝曉偟乿偲摨條丆暯柺撪偺懡廳愜傝偱偁傞偑丆巻柺摨巑偺娭學偐傜乽愜傝崬傒乿偑晄壜擻側応崌偑偁傝丆峏偵懡廳偵廳側偭偨乽愜傝崬傒乿偱偼愜傝曽偺岓曗偑暋悢懚嵼偡傞応崌偑偁傞丏杮僔僗僥儉偱偼愜傝巻傪廳側傝弴彉傪帩偮柺偺廤崌偲偟偰昞尰偟偰偍傝丆捀揰偺堏摦偵傛傝愜傝憖嶌傪峴側偆偺偱丆暋悢岓曗偺乽愜傝崬傒乿偐傜偺桞堦偺慖戰傗丆乽愜傝曉偟乿偲乽愜傝崬傒乿偺慖戰偼捀揰偺堏摦愭偑摨堦偲側傞偨傔偙傟傜偺巜掕偑峏偵昁梫偲側傞丏幚嵺偵偼愜傜傟傞慡偰偺柺偺夞揮晹暘偺宍忬偑摨堦偱懳徧揑偵愜傝崬傓応崌偑懡偄偺偱丆乽愜傝崬傒乿憖嶌傪偙偺傛偆側応崌偵尷掕偟偨丏傑偨丆乽愜傝曉偟乿偲乽愜傝崬傒乿偺慖戰偵偮偄偰偼儃僞儞偺 On, Off 偺忬懺偵傛傝巜掕偡傞偙偲偲偟偨丏乽愜傝崬傒乿偑壜擻偱偁傞偐偳偆偐偺敾掕偵偮偄偰偼丆偐側傝暋嶨偱條乆側応崌傪峫椂偡傞昁梫偑偁傝寁嶼張棟偑朿戝偲側傞偺偱峴側傢側偄偙偲偲偟偨丏僆儁儗乕僞偼帺暘偺摢偺拞偱愜傝偑壜擻偐偳偆偐傪僀儊乕僕偱偒傞偺偱丆偙傟偼幚嵺偺憖嶌偵偍偄偰偼偦傟傎偳廳梫側栤戣偲偼側傜側偐偭偨丏
偙傟傜偺婎杮揑側愜傝曽傪慻傒崌傢偣傞偙偲偵傛傝暋嶨側懡廳愜傝傕幚尰偱偒傞乮恾俀乯丏
 |  |
| (a) 愜傝曉偟 | (b) 愜傝嬋偘 |
 | |
| (c) 愜傝崬傒 | |
恾侾丂俁庬椶偺婎杮愜傝

恾俀丂婎杮愜傝偺慻傒崌傢偣偵傛傞暋嶨側愜傝曽
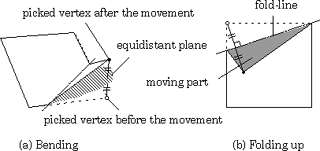
恾俁丂柺偺愜傟慄偲愜傝嬋偘妏搙
(1) 捀揰偺慖戰
儅僂僗偺拞墰儃僞儞傪墴偟偨弖娫偵 Picker偺忬懺偑'PICK'偵曄傢傝丆巻柺偺慡偰偺捀揰偺偆偪偐傜慖戰偝傟偨桞堦偺捀揰 (慖戰捀揰) 偑Picker偵傛傝Pick偝傟傞丏偙偺帪Picker偺埵抲偼慖戰捀揰偺埵抲 (慖戰捀揰偺堏摦尦) 偵曄峏偝傟傞丏Picker傪惂屼偟偰捀揰偺嬻娫揑側埵抲傪惓妋偵巜掕偡傞偙偲偼擄偟偄偨傔丆俀師尦偺僗僋儕乕儞搳塭憸忋偱Picker偐傜嵟傕嬤偄捀揰傪慖戰捀揰偲偡傞偙偲偵偡傞丏岓曗偑暋悢懚嵼偡傞応崌偼捀揰偺懏偡傞柺偺弴彉偑帇揰偐傜嵟傕嬤偄傕偺傪慖戰偡傞傛偆偵偡傞丏
(2) 捀揰偺堏摦
儃僞儞傪墴偟偰偄傞娫 (Picker偺忬懺'PICK'帪) Picker偺堏摦偵敽偄帺摦揑偐偮拃師揑偵丆慖戰捀揰偺堏摦愭嵗昗偺妉摼丆偦傟偵廬偆愜傟慄偲愜傝嬋偘妏搙偺寛掕丆愜傝寢壥偺僗僋儕乕儞傊偺昞帵偑峴側傢傟傞丏偙偺斀暅偼旕忢偵抁偄帪娫娫妘偱峴側傢傟傞偺偱丆僆儁儗乕僞偼僗儉乕僘偵曄宍偡傞愜傝巻傪娤應偟側偑傜丆儅僂僗傪憖嶌偟捀揰傪捈愙堏摦偡傞偙偲偵傛傝愜傟慄偲愜傝嬋偘妏搙傪儕傾儖僞僀儉偱帺桼偵曄壔偝偣傞偙偲偑偱偒傞丏
(3) 捀揰偺夝曻
儃僞儞傪棧偟偨弖娫偵Picker偺忬懺偑'RELEASE'偵曄傢傝丆慖戰捀揰偺堏摦愭偑屌掕偝傟丆偙偺帪偺愜傝寢壥偑愜傝庤弴偺僸僗僩儕乕偵搊榐偝傟傞丏埲屻Picker偼捀揰偲棧傟偰扨撈偱堏摦偡傞丏
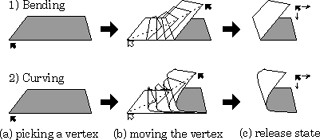
恾係丂儅僂僗僨僶僀僗偵傛傞婎杮憖嶌
(1) 捀揰摨巑傪廳偹崌傢偣偰愜傞
慖戰捀揰偲偁傞掱搙嬤偄捀揰偑懚嵼偡傟偽慖戰捀揰偺埵抲傪偦偺捀揰偺埵抲偵曄峏偡傞丏
(2) 曈摨巑傪廳偹崌傢偣偰愜傞
慖戰捀揰傪娷傓曈偲偁傞掱搙嬤偄曈偑懚嵼偡傟偽丆偦傟傜俀曈偑摨堦捈慄忋偱廳側傞傛偆偵捀揰偺埵抲傪曄峏偡傞丏俀曈偺嫍棧偵偼堦曽偺曈偲丆懠曽偺曈偺椉抂揰偲偺嫍棧傪棙梡偟偰偄傞丏
(3) 愜傟慄偑偁傞俀偮偺捀揰傪捠傞
愜傟慄偐傜偁傞掱搙嬤偄捀揰偑俀揰懚嵼偡傟偽丆愜傟慄偑偦偺俀揰傪捠傞傛偆偵捀揰偺埵抲傪曄峏偡傞丏
(4) 婎弨妏搙偱愜傝嬋偘傞
愜傝嬋偘妏搙偑90亱枖偼180亱(婎弨妏搙) 偵偁傞掱搙嬤偄側傜偽丆愜傝嬋偘妏搙偑偦偺婎弨妏搙偲側傞傛偆偵捀揰偺埵抲傪曄峏偡傞丏婎弨妏搙偵180亱傪壛偊傞偙偲偵傛傝丆乽愜傝曉偟乿丆乽愜傝崬傒乿偺暯柺愜傝傪梕堈偵偟偰偄傞丏傑偨丆愜傝嬋偘妏搙傪180亱埲壓偵惂尷偟帇揰懁偵偟偐愜傝嬋偘傜傟側偄傛偆偵僀儞僞儔僋僔儑儞傪扨弮壔偡傞偙偲偵傛傝丆峏偵愜傝憖嶌傪梕堈偵偟偰偄傞丏
偙傟傜偺曗惓婡擻偑摥偔偲僆儁儗乕僞偼丆椺偊偽捀揰傗曈摨巑偑屳偄偵堷偒崌偆傛偆偵丆捀揰偵栚偵尒偊側偄堷椡偑摥偄偰偄傞偐偺傛偆偵姶偠傜傟傞丏偙偺寢壥丆幚嵺偵巻傪愜傞傛傝傕惓妋偐偮恦懍偵壖憐偺巻傪愜傞偙偲偑壜擻偵側傞丏傑偨丆偙傟傜偺曗惓傪夝彍偟偨偄応崌偵偼儅僂僗傪戝偒偔堏摦偡傟偽傛偄丏
3. 愜傝巻偺偨傔偺僨乕僞峔憿
杮復偱偼愜傝憖嶌偵傛傝曄壔偟偰偄偔愜傝巻偺忬懺傪惓妋偵婰弎偡傞偨傔偺僨乕僞峔憿偵偮偄偰弎傋傞丏愜傝巻偼愜傟慄偵傛傝暘妱偝傟偨暋悢偺柺偺廤崌偱偁傝丆婎杮揑偵僒乕僼僃僀僗儌僨儖偱昞尰偟偰偄傞丏僨乕僞慡懱偼柺憌丆曈憌丆捀揰憌偲屇偽傟傞俁偮偺僨乕僞憌偵傛傝峔惉偝傟偰偄傞丏
(1) 擇暘栘儕僗僩峔憿
愜傝巻偼侾夞偺愜傝憖嶌偵傛傝偄偔偮偐偺柺偑俀暘妱偝傟傞偺偱丆柺忣曬偺婰壇偵偼婎杮揑偵擇暘栘偺儕僗僩峔憿偑揔偟偰偄傞丏侾偮偺柺偺忣曬傪帩偮柺僙儖偑栘偺愡偵埵抲偟丆柺偺俀暘妱偺嵺偵偼懳墳偡傞僙儖偵巕偺僙儖偑俀偮惗惉偝傟丆偦傟傜偑暘妱屻偺俀偮偺柺傪昞偡丏梩偺僙儖偺廤崌偑尰嵼偺愜傝巻偺忬懺傪丆栘峔憿慡懱偑愜傝憖嶌偵傛傞柺暘妱偺夁掱偺慡忣曬傪昞偟偰偄傞丏
(2) 柺僌儖乕僾偲柺僗僞僢僋
夁嫀偺乽愜傝嬋偘乿偵傛傝慡偰偺柺偑摨堦暯柺忋偵側偄応崌丆摨堦暯柺忋偺柺傪僌儖乕僾壔偡傞偙偲偵傛傝慡偰偺柺偼偄偔偮偐偺僌儖乕僾 (柺僌儖乕僾) 偵暘偗傜傟傞丏奺僌儖乕僾偵偼摨堦暯柺忋偵偁傞暋悢偺柺偵廳側傝弴彉 (柺斣崋) 傪梌偊傞柺僗僞僢僋偑偁傝丆慡偰偺柺僙儖偼偄偢傟偐偺僌儖乕僾偺柺僗僞僢僋偵懏偡傞丏恾俆(d)偱俁偮偺柺偺偆偪柺F1偼扨撈偱侾偮偺僌儖乕僾傪宍惉偡傞丏柺僙儖儖僢僋傾僢僾僥乕僽儖偼僌儖乕僾斣崋丆柺斣崋偵傛傝懳墳偡傞柺僙儖傪柺僙儖僣儕乕偐傜崅懍偵専嶕偡傞丏
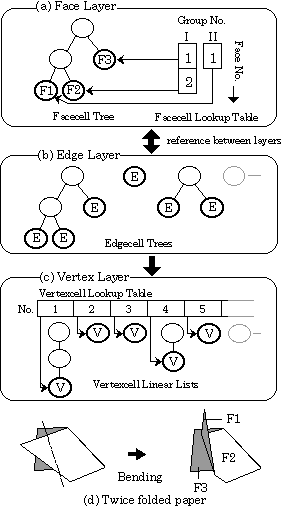
恾俆丂侾枃偺愜傝巻傪昞尰偡傞偨傔偺僨乕僞峔憿
恾俇丂柺偺暘妱偵敽偆僙儖偺峏怴
4. 儕僗僩偺峏怴
慜復偱弎傋偨儕僗僩峔憿偺僨乕僞孮偼愜傝憖嶌偺嵺偵峏怴偝傟傞丏杮復偱偼僨乕僞儕僗僩偺峏怴庤懕偒偵偮偄偰弎傋傞丏
嘆慖戰捀揰傪娷傓柺偼柧傜偐偵堏摦柺偱偁傞乮恾俈偺柺F1乯丏
嘇偁傞柺偑堏摦柺側傜偦偺柺偺堏摦晹暘偵偍偄偰曈傪嫟桳偡傞柺偼堏摦柺偱偁傞乮恾俈偺柺F2乯丏
嘊乽愜傝曉偟乿乽愜傝嬋偘乿偺応崌丆偁傞柺偑堏摦柺側傜偦偺柺偲丆柺偺夞揮偟偰偄偔懁偱堏摦晹暘偑廳側傞柺偼堏摦柺偱偁傞丏
嘋乽愜傝崬傒乿偺応崌丆偁傞俀偮偺柺偑堏摦柺側傜偦偺俀柺偺娫偵偁傝丆偦傟傜偺柺偺堏摦晹暘偲廳側傝偑偁傞柺偼堏摦柺偱偁傞丏
嘍 嘆乣嘋偺庤弴偵傛傝堏摦柺偲側傜側偐偭偨柺偼晄摦柺偱偁傞乮恾俈偺柺F3乯丏
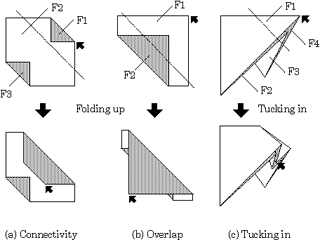
恾俈丂愜傝憖嶌偵偍偗傞俁庬椶偺柺
嘆 F0 偺暘妱偵敽偄柺僙儖 F1, F2 偍傛傃曈僙儖 E4 偑怴偟偔惗惉偝傟丆E4 傪娷傓柺偑 F1, F2 偵寛掕偝傟傞丏偨偩偟 E4 偼怴偟偄曈僙儖僣儕乕偺崻偱偁傞丏
嘇 E1 偺暘妱偵敽偄曈僙儖 E11, E12 偍傛傃捀揰僙儖 V4 偑怴偟偔惗惉偝傟丆E11, E12 偺撪梕偲 E4 偺侾偮偺抂揰偑寛掕偡傞丏傑偨 E11, E4 偑 F1 偺峔惉曈偵 E4, E12 偑 F2 偺峔惉曈偵壛偊傜傟傞丏V4 偺嵗昗傕偙偺帪偵寁嶼偝傟捀揰僙儖儖僢僋傾僢僾僥乕僽儖偵搊榐偝傟傞丏
嘊 E2 傪娷傓柺偺侾偮偑 F0 偐傜 F2 偵曄峏偝傟丆E2 偑 F2 偺峔惉曈偵捛壛偝傟傞丏傑偨 E4 偺巆傝偺抂揰偑 V3 偵寛掕偝傟傞丏
嘋 E3 傪娷傓柺偺侾偮偑 F0 偐傜 F1 偵曄峏偝傟丆E3 偑 F1 偺峔惉曈偵捛壛偝傟傞丏
峏怴庤懕偒偼曈偺悢偑4埲忋偺柺偵偮偄偰傕摨偠梫椞偱偁傞丏傑偨懡廳愜傝偺嵺偵偼慡偰偺暘妱柺偵懳偟偰峏怴庤懕偒偑峴側傢傟傞丏
 | 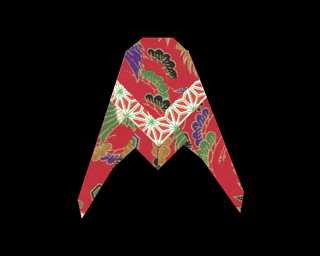 |
| (a) KABUTO | (b) Cicada |
 |  |
| (c) Plane | (d) Crane |
 | |
| (e) Yomiuri Press Jun 24, 1994 | |
恾俉丂嶌惉椺
5. 傓偡傃
杮暥偱偼丆愜傝巻偵懳偡傞壖憐暔懱憖嶌傪幚尰偟丆僌儔僼傿僢僋僗娐嫬偵偍偄偰幚暔姶妎偱憖嶌偑峴側偊傞儅儞儅僔儞僀儞僞僼僃僀僗偺壜擻惈傪帵偟偨丏愜傝巻傪擇暘栘儕僗僩偺峔憿偵傛傝娙寜偵婰弎偟偨寢壥丆巻偺忬懺曄壔偵懳偡傞僨乕僞偺峏怴傪儕傾儖僞僀儉偱崅懍偵峴偆偙偲偑偱偒偨丏傑偨儅僂僗偵傛傞嵗昗擖椡偺濨枂側柺傪帺摦揑偵曗惓偡傞偙偲偵傛傝丆僆儁儗乕僞偑堄恾偡傞憖嶌傪妋幚偵峴偆偙偲偑偱偒偨丏
杮僔僗僥儉偱偼暔懱偺憖嶌揰偑1揰偱偁傞偨傔愜傝曽偵偐側傝偺惂栺傪梌偊傞偙偲偵側偭偨丏彨棃揑偵偼憖嶌揰傪暋悢偵偡傞偙偲偵傛傝愜傝曽偺僶儕僄乕僔儑儞傪憹傗偟偨傝丆巻帺懱傪抏惈側偳偺暔棟揑惈幙傪梌偊偰婰弎偡傞偙偲偵傛傝峏偵幚暔偵嬤偄傕偺偵偡傞偙偲側偳傕峫偊偰偄傞丏
幱帿
擔崰擬怱偵屼巜摫丄屼摙榑捀偔尋媶幒偺奆條偵姶幱偟傑偡丅
嶲峫暥專